Students can access the NCERT MCQ Questions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables with Answers Pdf free download aids in your exam preparation and you can get a good hold of the chapter. Use MCQ Questions for Class 10 Maths with Answers during preparation and score maximum marks in the exam. Students can download the Pair of Linear Equations in Two Variables Class 10 MCQs Questions with Answers from here and test their problem-solving skills. Clear all the fundamentals and prepare thoroughly for the exam taking help from Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables Objective Questions.
Pair of Linear Equations in Two Variables Class 10 MCQs Questions with Answers
Students are advised to solve the Pair of Linear Equations in Two Variables Multiple Choice Questions of Class 10 Maths to know different concepts. Practicing the MCQ Questions on Pair of Linear Equations in Two Variables Class 10 with answers will boost your confidence thereby helping you score well in the exam.
Explore numerous MCQ Questions of Pair of Linear Equations in Two Variables Class 10 with answers provided with detailed solutions by looking below.
Question 1.
Find the dimensions of a garden, whose length is 4 m more than its width and half the perimeter is 36 m.
(a) 20 m × 16 m
(b) 14 m × 10 m
(c) 26 m × 22 m
(d) 12 m × 8 m
Answer
Answer: (a) 20 m × 16 m
l = b + 4
l + b = 36
l = 20 and, b = 6
Question 2.
The sides of a triangle are AB, BC and AC whose equations are respectively y-2 = 0; y = 3x – 7 and 2y + x = 0, The coordinates of points A and B are :
(a) A(3,2), B(-4,2)
(b) A(-4,2), B(3,2)
(c) A(3,2), B(2,-l)
(d) A(-4,2), B(2, -1)
Answer
Answer: (b) A(-4,2), B(3,2)
Equation of line AB : y – 2 = 0 Equation of line BC: y = 3 x -7 Equation of line AC: 2y + x = 0 Coordinates of point B can be obtained by solving AB and BC => (3,2).
Coordinate of point A are (- 4, 2)
A (- 4,2) and B(3,2)
Question 3.
Given is the system of Inconsistent equations, 2x + 7y = 11 and 5x + ky – 25 = 0, find k.
(a) – \(\frac{35}{2}\)
(b) 4
(c) \(\frac{35}{2}\)
(d) – 4
Answer
Answer: (c) \(\frac{35}{2}\)
\(\frac{a1}{a2}\) = \(\frac{b1}{b2}\) ≠ \(\frac{c1}{c2}\)
\(\frac{2}{5}\) = \(\frac{7}{k}\)
2k = 35
k = \(\frac{35}{2}\)
Question 4.
10 students of class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys who took part in the quiz.
(a) 3
(b) 7
(c) 2
(d) 8
Answer
Answer: (a) 3
No. of boys = x
and No. of girls = y
x + y =10
y = x + 4
x = 3
y = 7
=> Number of boys = 3
Question 5.
5 pencils and 7 pens together cost Rs. 50 whereas 7 pencils and 5 pens cost Rs. 46. Find the cost of 2 pencils and 3 pens.
(a) Rs. 42
(b) Rs. 39
(c) Rs. 21
(d) Rs. 16
Answer
Answer: (c) Rs. 21
Let, cost of 1 pencil = x and cost of 1 pen = y – 2
Cost of 2 pencil and 3 pens = 6 +15 = Rs. 21
=> Correct option is (c)
Question 6.
A linear equation in two variables has:
(a) 1 solution
(b) 2 solutions
(c) no solution
(d) infinitely many
Answer
Answer: (d) infinitely many
A linear equation in two variables has infinite number of solutions.
=> Correct option is (d)
Question 7.
A pair of linear equations is not consistent if:
(a) if has one solution
(b) it has many solutions
(c) graph intersect or coincide
(d) graph is parallel
Answer
Answer: (d) graph is parallel
37. Correct option is (d)
Question 8.
In a AABC, ∠A = x°, ∠B = (3a – 2)° and ∠C = y°. Also, ∠C – ∠B = 9°. Find the value of ∠B.
(a) 73°
(b) 82°
(c) 25°
(d) 49°
Answer
Answer: (a) 73°
∠A + ∠B + ∠C = 180°
=> x + (3x – 2) + y = 180
4x + y = 182 …(1)
y – 3x + 2 = 9 …(2)
Solving (1) & (2), y = 82, x = 25° => ∠B = 73°
Question 9.
The perimeter of a rectangle is 44 cm. Its length exceeds twice its breadth by 4 cm. Find the area of the rectangle.
(a) 46 cm²
(b) 49 cm²
(c) 96 cm²
(d) 69 cm²
Answer
Answer: (c) 96 cm²
Let, Length = x cm
Breadth = y cm
=> 2(x + y) = 44
=> x + y =221, y = 6 cm ,x = 16 cm
x = 2y+4
=> Area = 16 x 6 = 96 cm²
Question 10.
For what value of k, will the equations, x + 2y + (11 – k) = 0 and 2x + ky + (10 + k) = 0 represent the coincident lines :
(a) k = 12
(b) k = 4
(c) k = 36
(d) k = 2
Answer
Answer: (b) k = 4
\(\frac{a1}{a2}\) = \(\frac{b1}{b2}\) = \(\frac{c1}{c2}\)
\(\frac{1}{2}\) = \(\frac{2}{k}\) = \(\frac{11 – k}{10 + k}\)
k = 4
Question 11.
An equation ax + by + c = 0 is a linear equation in 2 variables, where a, b, c are :
(a) natural numbers
(b) whole numbers
(c) integers
(d) real numbers
Answer
Answer: (d) real numbers
Question 12.
Read the following graphs carefully, and match the following:
 |
Lines do not intersect | Unique solutions | Consistent with many solutions |
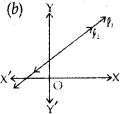 |
Lines intersect at 1 point | Infinite solutions | Consistent |
 |
Lines are coincident | No solutions | Parallel lines |
Answer
Answer:
 |
Lines intersect at 1 point | Unique solutions | Consistent |
 |
Lines are coincident | Infinite solutions | Consistent with many solutions |
 |
Lines do not intersect | No solutions | Parallel lines |
Question 13.
The pair of equations y = 9 and y = – 7 has:
(a) one solution
(b) two solutions
(c) infinitely many
(d) no solution solutions
Answer
Answer: (d) no solution solutions
y = 9 and y = – 7 are lines parallel to X-axis, thus these are parallel lines and hence no solution
Question 14.
The system of equations 3x – 5y = 20 and 6x – 10y = 40 has :
(a) one solution
(b) exactly 2 solutions
(c) infinitely many solutions
(d) no solutions solutions
Answer
Answer: (c) infinitely many solutions
\(\frac{a1}{a2}\) = \(\frac{b1}{b2}\) = \(\frac{c1}{c2}\) = \(\frac{x}{y}\)
Question 15.
For what value of a, the pair of equations, 3x + 2y – 4= 0 and ax – y – 3 = 0 has a unique solutions :
(a) All real numbers except – \(\frac{3}{2}\)
(b) a=- \(\frac{3}{2}\)
(c)a= \(\frac{3}{2}\)
(d)a= \(\frac{2}{3}\)
Answer
Answer: (a) All real numbers except – \(\frac{3}{2}\)
For unique solutions , \(\frac{a1}{a2}\) ≠ \(\frac{b1}{b2}\)
a ≠ – \(\frac{3}{2}\)
a can all possible values except – \(\frac{3}{2}\)
Question 16.
The sum of a two digit number is 8. The number obtained by reversing the digits exceeds the number by 18. Then the given number is :
(a) 53
(b) 35
(c) 26
(d) 62
Answer
Answer: (b) 35
Let, the digit at units’ place = x and digit at ten’s place = y => x + y = 8 and lOx + y = 18 + (10y + x)
No. = 35.
Question 17.
In a triangle, the sum of two angles is equal to the third angle. If the difference between two angles is 30°, find the angles.
(a) 15°, 45°, 75°
(b) 20°, 50°, 80°
(c) 30°, 60°, 90°
(d) 45°, 45°, 90°
Answer
Answer: (c) 30°, 60°, 90°
(x) + (y) + (x + y) 180°
x + y = 90°
x – y = 30°
=> x = 60°, y = 30°
=> Angles are 30°, 60° and 90°
Read the graph carefully and answer the questions given (Q.No. 18 to Q. No. 22):
Question 18.
(a) (0,1)
(b) (4,0)
(c) (2,3)
(d) (0,6)
Answer
Answer: (b) (4,0)
Correct option is (b).
Question 19.
The line x – y + 1 = 0 meets Y-axis at:
(a) (0,1)
(b) (4,0)
(c) (2,3)
(d) (0,6)
Answer
Answer: (a) (0,1)
Correct option is (a).
Question 20.
The solutions of the system of equations, x – y + 1 = 0, 3x + 2y -12 = 0 is :
(a) (0,1)
(b) (4,0)
(c) (2,3)
(d) (0,6)
Answer
Answer: (c) (2,3)
Since the two lines meet at (2, 3)
Correct option is (c).
Question 21.
The area of triangle formed by x-y +1 = 0, 3x + 2y -12 = 0 and X-axis is :
(a) \(\frac{15}{2}\) sq. units
(b) 9 sq. units
(c) 5 sq. units
(d) 6 sq. units
Answer
Answer: (a) \(\frac{15}{2}\) sq. units
Area of ∆ formed by x – y +1 = 0,3x + 2y – 12 = 0 and X-axis is, (∆ABC)
\(\frac{1}{2}\) × 5 × 3 = \(\frac{15}{2}\)sq. units
Question 22.
The area of triangl e formed by x – y +1 = 0, 3x + 2y -12 = 0 and x = 0 is :
(a) \(\frac{15}{2}\) sq. units
(b) 9 sq. units
(c) 5 sq. units
(d) 6 sq. units
Answer
Answer: (c) 5 sq. units
Area required = Area (∆ECD)
= \(\frac{15}{2}\) × 5 × 2 = 5 sq. units
Question 23.
Find the value of (x + y) if 148x + 231y=527 and 231x + 148y = 610.
(a) 3
(b) 480
(c) 1
(d) 481
Answer
Answer: (a) 3
Adding the given equations,
379x + 379y = 1137
x + y = 3
Question 24.
The line x = 4 :
(a) passes through origin
(b) parallel to X-axis
(c) parallel to Y-axis
(d) does not meet Y-axis at all
Answer
Answer: (c) parallel to Y-axis
x = 4 is a line parallel to Y-axis

Question 25.
If x and y satisfy the given two equations, 4x + \(\frac{6}{y}\) = 15, 6x – \(\frac{8}{y}\) = 14; find p is y = px – 2.
(a) 1
(b) 2
(c) 3
(d) \(\frac{4}{3}\)
Answer
Answer: (d) \(\frac{4}{3}\)
4x + \(\frac{6}{y}\) = 15
6x – \(\frac{8}{y}\)= 14
=> x = 3
=> y = px – 2
y = 2
=> 2 = 3p – 2
=> Correct option is (d).
Question 26.
Find the value which k cannot take, for the given system to have a unique solutions, x + 2y = 3, ky + 5x + 7 = 0.
(a) 10
(b) \(\frac{- 14}{3}\)
(c) any real
(d) any real number
number except 10.
Answer
Answer: (a) 10
\(\frac{a1}{a2}\) = \(\frac{1}{5}\), \(\frac{b1}{b2}\) = \(\frac{2}{k}\), \(\frac{c1}{c2}\) = – \(\frac{3}{7}\)
\(\frac{a1}{a2}\) ≠ \(\frac{b1}{b2}\)
k ≠ 10
Question 27.
Find p and q so that given system has infinite number of solutions, 4x + 6y -14 = 0.
(p + q)x + (2 p – q)y – 3 (p + q +1) = 0
(a)p = 1, q = 1
(b)p = 1,q = – 1
(c) p = 1, q = 5
(d) p = 5, q = 1
Answer
Answer: (d) p = 5, q = 1
System will have infinite solutions, if
\(\frac{b1}{b2}\) = \(\frac{b1}{b2}\) = \(\frac{b1}{b2}\)
p – 5q = 0 and p + q = 6
p = 5
q = 1
=> Correct option is (d).
Question 28.
Find x and y in the given rectangle :

(a) x = 1, y = 4
(b) x = 4, y = 1
(c) x = 2, y = 2
(d) x = 3, y = 1
Answer
Answer: (a) x = 1, y = 4
3x + y = 7 => 3x + y = 7
x + 3y = 13 => 3x + 9y = 39
x = 1; y = 4
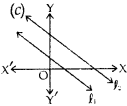
Read the figure carefully and answer fhe following questions (Q. No. 29 to Q. No. 33):

Question 29.
Equation of line l is,
(a) x = – 2
(b) x = 2
(c)y = 2
(d) y = – 2
Answer
Answer: (a) x = – 2
Line l is parallel to Y-axis at a distance of 2 units in the negative direction
=> Equation of line / is x = – 2
=> Correct option is (a).
Question 30.
Equation of line m is :
(a) x = – 2
(b) x = 2
(c) y = 2
(d) y = – 2
Answer
Answer: (c) y = 2
y = 2 => Correct option is (c).
Question 31.
The figure obtained by lines l, m, X-axis and Y-axis, can not be the :
(a) square
(b) rectangle
(c) trapezium
(d) triangle
Answer
Answer: (d) triangle
The figure obtained is square. Since every square is a rectangle and is a trapezium also.
Thus, the wrong name is triangle
=> Correct option is (d).
Question 32.
Area of figure OABC is (in square units):
(a) 1
(b) 2
(c) 3
(d) 4
Answer
Answer: (d) 4
Area of figure OABC = 4 square units
=> Correct option is (d).
Question 33.
Coordinates of A, B, C (in order) are:
(a) (2,0), (2,-2) (0,-2)
(b) (0,2), (-2,2), (-2,0)
(c) (-2,0), (2,2), (0,-2)
(d) (0,2), (2,2), (0,-2)
Answer
Answer: (b) (0,2), (-2,2), (-2,0)
A(0,2), B(-2,2), C(-2,0).
=> Correct option is (b).
Question 34.
Find the values of x and y if ABCD is a cyclic quadrilateral, ∠A = 6x + 10°, ∠B = (5x)°, ∠C = (x + y)° (∠D)=(3y-10)°.
(a) x = 30°, y = 20°
(b) x = 20°, y = 30°
(c) x = 40°, y = 10°
(d) x = 10°, y = 40°
Answer
Answer: (b) x = 20°, y = 30°
ABCD is cyclic
=> ∠A + ∠C = 180° and ∠B + ∠D = 180°
=> 6x + 10 + x + y = 180°
=> 7x + y = 170°
5x + 3y – 10 = 180°
=> 5x + 3y = 190°
x = 20°, y = 30° => Correct option is (b)
Question 35.
If x + 5y = 34 and x – 5y = – 6, find the value of 5y – 2x.
(a) – 8
(b) 14
(c) 8
(d) 20
Answer
Answer: (a) – 8
x + 5y = 34
x – 5y = – 6
x=14
Solving these,
x = 14; y = 4
=> Correct option is (a).
Question 36.
Find the value of λ = \(\frac{x}{y}\) if bx – ay = a + bax + by = a-b.
(a) 2
(b) 1
(c) 0
(d) – 1
Answer
Answer: (d) -1
ax + by=a – b
bx – ay =a + b
Solving these
x = 1
y = – 1
λ = \(\frac{x}{y}\) = – 1
Question 37.
The given system of equations,
– x + 2y + 2 = 0
\(\frac{1}{2}\)x – \(\frac{1}{4}\)y – 1= o, has :
(a) a unique solution
(b) infinite solutions
(c) no solution
(d) 2 solutions
Answer
Answer: (a) a unique solution
\(\frac{a1}{a2}\) = \(\frac{- 1}{1/2}\) = 2
\(\frac{b1}{b2}\) = \(\frac{2}{- 1/4}\) = – 8
since \(\frac{a1}{a2}\) ≠ \(\frac{b1}{b2}\) Given system of equations has a unique solution.
Question 38.
The pair of equations x = a and y = b graphically represents lines which are:
(a) parallel
(b) intersecting at (b, a)
(c) intersecting at (a, b)
(d) coincident
Answer
Answer: (c) intersecting at (a, b)
x = a and y = b graphically represents lines which are intersecting at (a, b)
=> Correct option is (c).
Question 39.
If x = a and y = b is the solution of the (a) coincident .equations \(\frac{4}{x}\) + 3y = 14 and \(\frac{3}{x}\) – 4y = 23, then the values of a and b are respectively:
(a) – 2 and 5
(b) 5 and – 2
(c) \(\frac{1}{5}\) and – 2
(d) 5 and – \(\frac{1}{2}\)
Answer
Answer: (c) \(\frac{1}{5}\) and – 2
let, \(\frac{1}{x}\) = u
4 u + 3 y =14
3u □ 4y = 23
u = 5
y = – 2
x = \(\frac{1}{5}\)
y = – 2
Question 40.
One equation of a pair of dependent linear equations is -5x + 7y = 2. The second equation can be:
(a) 10x + 14y + 4 = 0
(b) – 10x – 14y + 4 = 0
(c) – 10x + 14y + 4 = 0
(d) 10x – 14y = – 4
Answer
Answer: (d) 10x – 14y = – 4
\(\frac{a1}{a2}\) = \(\frac{b1}{b2}\) = \(\frac{c1}{c2}\)
Question 41.
The pair of equations y = 0 and y = – 7 has :
(a) no solution
(b) infinitely many solutions
(c) one solution
(d) two solutions
Answer
Answer: (a) no solution
Question 42.
Which of the following is not a solution of pair of equations 3x – 2y = 4 and 6x – 4y = 8?
(a) x = 5, y = 3
(b) x = 2, y = 1
(c) x = 6, y = 7
(d) x = 4, y = 4
Answer
Answer: (a) x = 5, y = 3
Question 43.
The pair of equations x = a and y = b graphically represents lines which are
(a) parallel
(b) intersecting at (b, a)
(c) coincident
(d) intersecting at (a, b)
Answer
Answer: (d) intersecting at (a, b)
Question 44.
One equation of a pair of dependent linear equations is – 5x + 7y = 2, the second equation can be :
(a) -10x + 14y + 4 = 0
(b) -10x – 14x + 4 = 0
(c) 10x – 14y = – 4
(d) 10x + 14y + 4 = 0
Answer
Answer: (c) 10x – 14y = – 4
Question 45.
Two equations in two variables taken together are called
(a) linear equations
(b) quadratic equations
(c) simultaneous equations
(d) none of these
Answer
Answer: (c) simultaneous equations
Question 46.
8 girls and 12 boys can finish work in 10 days while 6 girls and 8 boys can finish it in 14 days. Find the time taken by the one girl alone that by one boy alone to finish the work.
(a) 120, 130
(b) 140,280
(c) 240,280
(d) 100,120
Answer
Answer: (b) 140,280
Question 47.
The graph of y = 4x is a line
(a) parallel to x-axis
(b) parallel to y-axis
(c) perpendicular to y-axis
(d) passing through the origin
Answer
Answer: (d) passing through the origin
Question 48.
If the pair of equation has no solution, then the pair of equation is :
(a) inconsistent
(b) coincident
(c) consistent
(d) none of these
Answer
Answer: (a) inconsistent
Question 49.
Find the value of ‘a” for which the system of equations ax + 2y – 4 = 0 and x – y – 3 = 0 will represent intersecting lines?
(a) a ≠ -2
(b) a = -2
(c) a = 2
(d) a ≠ 2
Answer
Answer: (a) a ≠ -2
Question 50.
The pair of equations 3x + 4y = k, 9x + 12y = 6 has infinitely many solutions if –
(a) k = 2
(b) k = 6
(c) k = 6
(d) k = 3
Answer
Answer: (a) k = 2
Question 51.
If a pair of linear equations is consistent, then the lines will be
(a) always coincident
(b) parallel
(c) always intersecting
(d) intersecting or coincident
Answer
Answer: (d) intersecting or coincident
Question 52.
Which of following is not a solution of 3a + b = 12??
(a) (3, 3)
(b) (5, -3)
(c) (4, 0)
(d) (2, 4)
Answer
Answer: (d) (2, 4)
Question 53.
How many solutions of the equation 15x – 14y + 11 = 0 are possible?
(a) 2
(b) No solution
(c) 1
(d) Infinite
Answer
Answer: (d) Infinite
Question 54.
The pair of equations 3x – 5y = 7 and – 6x + 10y = 7 have
(a) a unique solution
(b) infinitely many solutions
(c) no solution
(d) two solutions
Answer
Answer: (c) no solution
Question 55.
The graph of y = 5 is a line parallel to the
(a) x-axis
(b) y-axis
(c) both axis
(d) none of these
Answer
Answer: (a) x-axis
Question 56.
The value of k, for which equations 3x + 5y = 0 and kx + lOy = 0 has a non-zero solution is
(a) 6
(b) 0
(c) 2
(d) 5
Answer
Answer: (a) 6
Question 57.
The present age of a father is the sum of the ages of his three sons. Ten years from now his age will be a three quarter of the sum of their ages then. How old is the father?
(a) 50 years
(b) 30 years
(c) 40 years
(d) 60 years
Answer
Answer: (a) 50 years
Question 58.
Find a and b for which (a – 1) x + 3y = 2, 6x + (1 – 2b) y = 6 infinite solution.?
(a) a = -7, b= -4
(b) a = -1, b = -4
(c) a = 3, b = -1
(d) a = 3, b = -4
Answer
Answer: (d) a = 3, b = -4
Question 59.
The graph of x = -2 is a line parallel to the
(a) x-axis
(b) y-axis
(c) both x- and y-axis
(d) none of these
Answer
Answer: (b) y-axis
Question 60.
The graph of the equation 2x + 3y = 5 is a
(a) vertical line
(b) straight line
(c) horizontal line
(d) none of these
Answer
Answer: (b) straight line
Question 61.
If am bl then the system of equations ax + by = c, lx + my = n, has
(a) a unique solution
(b) no solution
(c) infinitely many solutions
(d) none of these
Answer
Answer: (a) a unique solution
Question 62.
Find the solution to the following system of linear equations:
2x-5y+4 = 0 2x+y-8 = 0?
(a) (3,-2)
(b) (2,3)
(c) (-1,2)
(d) (3,2)
Answer
Answer: (d) (3,2)
Question 63.
Which of the following pair of linear equations is inconsistent??
(a) 2x + 3y = 7; 4x + 6y = 5
(b) x – 2y = 6; 2x + 3y = 4
(c) 9x – 8y = 17; 18x -16y = 34
(d) 5x – 3y =11; 7x + 2y =13
Answer
Answer: (a) 2x + 3y = 7; 4x + 6y = 5
Question 64.
Find the solution to the following system of linear equations:
2p+3q = 9 p – q = 2?
(a) (4,2)
(b) (3,1)
(c) (2,-3)
(d) (-4,1)
Answer
Answer: (b) (3,1)
Question 65.
If x = a, y = b is the solution of the equations x + y = 5 and 2x – 3y = 4, then the values of a and b are respectively
(a) 6, -1
(b) 2, 3
(c) 1, 4
(d) \(\frac { 19 }{ 5 }\), \(\frac { 6 }{ 5 }\)
Answer
Answer: (d) \(\frac { 19 }{ 5 }\), \(\frac { 6 }{ 5 }\)
Question 66.
The pair of linear equations 2kx + 5y = 7, 6x – 5y = 11 has a unique solution if
(a) k = -3
(b) k = 3
(c) k = 5
(d) k = -5
Answer
Answer: (a) k = -3
Question 67.
The pair of equations x = 0 and x = 5 has
(a) no solution
(b) unique/one solution
(c) two solutions
(d) infinitely many solutions
Answer
Answer: (c) two solutions
Question 68.
If A : Homogeneous system of linear equations is always consistent. R : x = 0, y = 0 is always a solution of the homogeneous system of equations with unknowns x and y, then which of the following statement is true?
(a) A is true and R is the correct explanation of A
(b) A is false and R is not a correrct explanation of A
(c) A is true and R is false
(d) A is false and R is true
Answer
Answer: (a) A is true and R is the correct explanation of A
We believe the knowledge shared regarding NCERT MCQ Questions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables with Answers Pdf free download has been useful to the possible extent. If you have any other queries regarding CBSE Class 10 Maths Pair of Linear Equations in Two Variables MCQs Multiple Choice Questions with Answers, feel free to reach us via the comment section and we will guide you with the possible solution.