Polynomials Class 10 Extra Questions Maths Chapter 2 with Solutions Answers

Here you will find Polynomials Class 10 Extra Questions Maths Chapter 2 with Answers Solutions, Extra Questions for Class 10 Maths are solved by experts and will guide students in the right direction.

Extra Questions for Class 10 Maths Polynomials with Answers Solutions

Extra Questions for Class 10 Maths Chapter 2 Polynomials with Solutions Answers

Polynomials Class 10 Extra Questions Objective Type

Question 1.
The number of polynomials having zeroes -2 and 5 is:
(a) 1
(b) 2
(c) 3
(d) More than 3
Answer:
(d) More than 3

Question 2.
If 1 is zero of the polynomial p(x) = ax² – 3(a – 1)x – 1, then the value of ‘a’ is:
(a) 1
(b) -1
(c) 2
(d) – 2
Answer:
(a) 1

Question 3.
If a, ß are zeroes of x² – 6x + k. What is the value of k if 3a + 2B = 20.
(a) – 16
(b) 8
(c) – 2
(d) -8
Answer:
(a) – 16

Question 4.
If one zero of 2x² – 3x + k is reciprocal to the other, then the value of k is:
(a) 2
(b) \(\frac {-2}{3}\)
(c) \(\frac {-3}{2}\)
(d) -3
Answer:
(a) 2

Question 5.
If p(x) = x² + 6x + 9 and q(x) = x + 3 then remainder will be when p(x) is divided by q(x):
(a) – 1
(b) 0
(c) 11
(d) 2
Answer:
(b) 0

Question 6.
Dividing (x² + 1) by (x + 1), the remainder will be:
(a) -1
(b) 11
(c) 0
(d) – 2
Answer:
(c) 0

Question 7.
Dividing x³ + 3x + 3 by (x + 2), the remainder will be:
(a) -2
(b) -1
(c) 0
(d) 1
Answer:
(d) 1

Question 8.
The zero’s of the polynomial (x² – 2x – 3) will be:
(a) – 3, 1
(b) -3, -1
(c) 3, -1
(d) 3, 1
Answer:
(c) 3, -1
Solution:
x² – 2x – 3 = x² – 3x + x – 3
= x(x – 3) + 1 (x – 3 ) = (x – 3) (x + 1)
∴ Zeros of the polynomial are 3, -1
Hence, choice (c) is correct.

Question 9.
Dividing x³ – 3x² – x + 3 by x – 4x + 3 the remainder will be:
(a) – 3
(b) 3
(c) 1
(d) 0
Answer:
(d) 0

Polynomials Class 10 Extra Questions Very Short Answer Type

Question 1.
Find a quadratic polynomial each with the given numbers as the sum and product of the zeroes respectively.
(i) \(\frac {1}{4}\), -1
(ii) √2, \(\frac {1}{3}\)
(iii) 0, √5
(iv) 1, 1
(v) – \(\frac {1}{4}\), \(\frac {1}{4}\)
(vi) 4, 1
Solution:
Let the polynomial be ax² + bc + c and its zeroes be α and β.
(i) Here, α + β = \(\frac {1}{4}\) and αβ = -1
Thus, the polynomial formed = x² – (Sum of the zeroes)x + Product of the zeroes

If k = 4 then the polynomial is 4x² – 3 – 4.

(ii) Here, α + β = √2 and αβ = \(\frac {1}{3}\)
Thus, the polynomial formed = x² – (Sum of the zeroes) x + Product of the zeroes

If k = 3, then, the polynomial is 3x² – 3√2x + 1.

(iii) Here, α + β = 0 and aß = √5
Thus, the polynomial formed = x² – (Sum of the zeroes) x + Product of zeroes
= x² – (0)x + √5
= x² + √5

(iv) Let the polynomial be ax² + bx + c and its zeroes α and β. Then

If a = 1 then b = -1 and c = 1
∴ One quadratic polynomial which satisfy the given conditions is x² – x + 1.

(v) Let the polynomial be ax² + bx +c and its zeroes be a and B. Then,

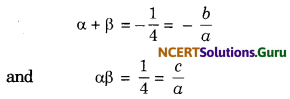
if a = 4, then b = 1 and c = 1.
∴ One quadratic polynomial which satisfy the given conditions is 4x² + x + 1.

(vi) Let the polynomial be ax² + bx + c and its zeroes be a and ß. then,

and αβ = 1 if a = 1 then b = -4 and c = 1
∴ One quadratic polynomial which satisfy the given conditions is x² – 4x + 1.

Question 2.
Divide p(y) by g(y) if p(y) = y³ – 3y² – y + 3 and g(y) = y² – 4y + 3.
Answer:
We write
y³ – 3y² – y + 3 = (y + 1) (y² – 4y + 3).
Solution:

Here, the quotient is y + 1 and the remainder is zero.

Question 3.
Examine if x – 1 is a factor of 2x³ – 5x + 3.
Solution:

Here, remainder is 0, hence, x – 1 is one factor of 2x³ – 5x + 3.

Polynomials Class 10 Extra Questions Short Answer Type

Question 1.
Divide the polynomial f(x) = 3x² – x³ – 3x + 5 by the polynomial g(x) = x – 1 – x² and verify the division alogrithm.
Solution:
f(x) = – x³ + 3x² – 3x + 5 and g(x) = – x² + x- 1

∴ Quotient = x – 2 and remainder = 3.
as dividend = Q x divisior + remainder
– x³ + 3x² – 3x + 5 = (x – 2)(-x² + x – 1) +3
= – x³ + x² – x + 2x² – 2x + 2 + 3
= – x³ + 3x² – 3x + 5
Verify

Question 2.
Divide 3 – x + 2x² by (2 – x) and verify alogrithm.
Solution:
First we write the terms of dividend and divisor in decreasing order of their degrees and then perform the division as shown below:

Clearly, degree (9) = 0 < degree (- x + 2).
∴ quotient = (- 2x – 3) and remainder = 9.
= (quotient x divisor) + remainder
= (- 2x – 3)(- x + 2) + 9
= 2x² – 4x + 3x – 6 + 9
= 2x² – x + 3
= dividend
Thus, (quotient x divisor) + remainder = dividend. Hence, the division algorithm is verified.

Question 3.
On dividing x³ – 3x² + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and – 2x + 4, respectvely. Find g(x).
Solution:
Given, p(x) = x² – 3x² + x + 2, q(x) = x – 2 and r(x) = – 2x + 4. By division algorithm, we know that
Dividend = Divisor × Quotient + Remainder
p(x) = q(x) × g(x) + r(x).
Therefore,
x³ + 3x² + x + 2 = (x – 2) × g(x) + (-2x + 4)
⇒ x³ – 3x² + x + 2 + 2x – 4 = (x – 2) × g(x)
⇒
On dividing x³ – 3x² + 3x – 2 by x – 2, we get

Hence, g(x) = x² – x + 1.

Question 4.
Divide 6x⁵ + 5x⁴ + 11x³ – 5x² + 2x + 7 by 3x² – 2x + 4.
Solution:

Question 5.
If – 3 is one of the zeros of the quadratic polynomial (k – 1) x² + kx + 1. Find the value of other zeros.
Solution:
Given that – 3 is one zeros of the polynomial
(k – 1) x² + kx + 1
∴ (k – 1)(-3)² + k (-3) + 1 = 0 .
⇒ 9k – 9 – 3k + 1 = 0
⇒ 6k = 8
⇒ Putting the value of k = \(\frac {4}{3}\) in given polynomial,
we get (\(\frac {4}{3}\)– 1) x² + \(\frac {4}{3}\) x + 1

⇒ x² + 4x + 3 = x² + 3x + x + 3
= x (x + 3) + 1 (x + 3)
⇒ (x + 3) (x + 1)
∴ zeros are – 3 and – 1
Hence their zeros of the quadratic polynomial is – 1.

Question 6.
Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg g(x)
(ii) deg g(x) = deg r(x)
(iii) deg q(x) = 0
Solution:
Let
q(x) = 3x² + 2x + 6,
degree of g(x) = 2
p(x) = 12x² + 8x + 24,
degree of p(x) = 2

(i) Using division algorithm,
We have,’ p(x) = (x) × g(x) + r(x)
On dividing 12x² + 8x + 24 by 3x² + 2x + 6.
we get

Since, the remainder is zero, therefore 3x² + 2x + 6 is a factor of 12x² + 8x + 24.
∴ g(x) = 4 and r(x) = 0.

(ii) p(x) = x⁵ + 2x⁴ + 3x³ + 5x² + 2
q(x) = x² + x + 1, degree of g(x) = 2
g(x) = x³ + x² + x + 1
r(x) = 2x² – 2x + 1, degree of r(x) = 2
Here, deg q(x) = deg r(x)
On dividing x⁵ + 2x⁴ + 3x³ + 5x² + 2 by x² + x + 1, we get

Here, g(x) = x³ + x² + x + 1
and r(x) = 2x² – 2x + 1

(iii) Let p(x) = 2x⁴ + 8x³ + 6x² + 4x + 12, r(x) = 2, degree of r(x) = 0
g(x) = x⁴ + 4x³ + 3x² + 2x + 1
⇒ 9(x) = 10
Here deg r(x) = 0
On dividing 2x⁴ + 8x³ + 6x² + 4x + 12 by 2,
we get

Question 7.
Find the zero’s of quadratic polynomial f(x) = 3x² – 3 – 4. Verify the relationship between the zeros and its coefficients.
Solution:
∴ f(x) = 3x² – x – 4
= 3x² – 4x + 3x – 4
= x(3x – 4) + 1 (3x – 4)
= (3x – 4) (x + 1)
∴ zero’s are \(\frac {4}{3}\) and -1.
sum of the zeros =

Question 8.
Solve the pair of linear simultaneous equations
2x – y = 1 and x + 2y = 13
By drawing their graphs. Find the coordinates of vertices of a triangle formed by these lines and y-axis.
Solution:
2x – y = 1 ⇒ x + 2y = 13
2x = 1 + y ⇒ x = 13 – 2y

Now plot the points on the graph paper.

The coordinate of required ∆ are
A(3, 5), B (0, \(\frac {13}{2}\)) and C(0, -1) respectively
Solution is x = 3, y = 5

Question 9.
Find all the zeros of polynomial 2x⁴ – 3x² – 3x² + 6x – 2. If two of its zeros are √2 and √2.
Solution.
quad. polynomial form by the given zeros is
(X – √2) (x + √2)
⇒ x² – 2
Now divided the given polynomial by x² – 2

∴ x⁴ – 3x³ – 3x² + 6x – 2
= (x² – 2) (2x² – 3x + 1)
= (x² – 2) (2x² – 2x – x + 1)
= (x² – 2) [2x(x -1) – 1(x-1)]
= (x √2 )(x + √2)(x – 1) (2x – 1)
Hence all zeros are
1/2, 1, √2 and – √2