Introduction to Trigonometry Class 10 Extra Questions Maths Chapter 8 with Solutions Answers

Here you will find Introduction to Trigonometry Class 10 Extra Questions Maths Chapter 8 with Answers Solutions, Extra Questions for Class 10 Maths are solved by experts and will guide students in the right direction.

Extra Questions for Class 10 Maths Introduction to Trigonometry with Answers Solutions

Extra Questions for Class 10 Maths Chapter 8 Introduction to Trigonometry with Solutions Answers

Introduction to Trigonometry Class 10 Extra Questions Objective Type

Question 1.
The value of \(\frac{2 \tan 30^{\circ}}{1-\tan ^{2} 30^{\circ}}\) will be:
(i) sin 60°
(ii) cos 60°
(iii) tan 60°
(iv) sin 30°
Answer:
(ii) cos 60°
Solution.

= 2 sin 30o. cos 30°
= sin 60°
Hence, Choice (ii) is correct

Question 2.
If sin θ = 1, the value of sin 20 will be :
(i) -1
(ii) 0
(iii) 1
(iv) 2
Answer:
(ii) 0

Question 3.
The value of cot (- 1470°) will be :
(i) –\(\frac{1}{\sqrt{3}}\)
(ii) – √3
(iii) \(\frac{1}{\sqrt{3}}\)
(iv) √3
Answer:
(ii) – √3

Question 4.
In triangle ABC, the value of sin (B + C) will be :
(i) sin B + sin C
(ii) sin A
(iii) 0
(iv) cos A
Answer:
(ii) sin A

Question 5.
The value of cos 15° is :
(i)
(ii)
(iii)
(iv)
Answer:
(i)

Question 6.
If sin θ = cosec θ and ≤ θ ≤ π then value of 0 will be :
(i) π
(ii) \(\frac{\pi}{2}\)
(iii) \(\frac{\pi}{4}\)
(iv) 0
Answer:
(ii) \(\frac{\pi}{2}\)

Question 7.
The value of cosec 810 will be :
(i) -1
(ii) 0
(iii) 1
(iv) ∞
Answer:
(iii) 1

Question 8.
Find the value of \(\frac{\sin ^{2} 15^{\circ}-\cos ^{2} 15^{\circ}}{\sin ^{2} 15^{\circ}+\cos ^{2} 15^{\circ}}\).
(i) 1
(ii) -1
(iii) \(\frac{2}{\sqrt{3}}\)
(iv) \(\frac{-\sqrt{3}}{2}\)
Answer:
(iv) \(\frac{-\sqrt{3}}{2}\)

Question 9.
The value of will be :
(i) \(\frac{1}{\sqrt{2}}\)
(ii) √2 – 1
(iii) √2
(iv) \(\frac{\sqrt{2}+1}{\sqrt{2}-1}\)
Answer:
(iii) √2

Question 10.
The value of sin 570° will be :
(i) \(\frac{-1}{2}\)
(ii) \(\frac{-\sqrt{3}}{2}\)
(iii) \(\frac{1}{2}\)
(iv) \(\frac{\sqrt{3}}{2}\)
Answer:
(i) \(\frac{-1}{2}\)

Question 11.
If tan A = \(\frac{1}{\sqrt{3}}\) and tan B = √3 then the value of tan (A + B) will be :
(i) 0
(ii) \(\frac{1}{\sqrt{3}}\)
(iii) 1
(iv) ∞
Answer:
(iv) ∞

Question 12.
If sin α = cos α then the value of α will be:
(i) 30°
(ii) 45°
(iii) 60°
(iv) 90°
Answer:
(ii) 45°

Question 13.
The value of sin2 θ +\(\frac{1}{1+\tan ^{2} \theta}\) is :
(i) cos² θ
(ii) sin² θ
(iii) 1
(iv) sec² θ
Answer:
(iii) 1

Question 14.
If sec θ = 2 then the value of θ will be :
(i) \(\frac{\pi}{2}\)
(ii) \(\frac{\pi}{3}\)
(iii) \(\frac{\pi}{4}\)
(iv) \(\frac{\pi}{6}\)
Answer:
(ii) \(\frac{\pi}{3}\)

Question 15.
The value of cos (-1920°) will be :
(i) – 1/2
(ii) 0
(iii) 1/2
(iv) 1
Answer:
(i) – 1/2

Question 16.
If 2 cos 30 = 1. Then the value of a will be :
(i) 30°
(ii) 45°
(iii) 60°
(iv) 20°
Answer:
(iv) 20°

Question 17.
The value of \(\frac{\sin 20^{\circ}}{\cos 70^{\circ}}\) will be :
(i) more than 1
(ii) 1
(iii) 0
(iv) less than 1
Answer:
(ii) 1

Question 18.
The value of sin (- 570°) is :
(i) –\(\frac{\sqrt{3}}{2}\)
(ii) \(\frac{\sqrt{3}}{2}\)
(iii) \(\frac{1}{2}\)
(iv) –\(\frac{1}{2}\)
Answer:
(iii) \(\frac{1}{2}\)

Question 19.
The value of sin 840° will be:
(i) \(\frac{1}{2}\)
(ii) –\(\frac{1}{2}\)
(iii) \(\frac{\sqrt{3}}{2}\)
(iv) –\(\frac{\sqrt{3}}{2}\)
Answer:
(iii) \(\frac{\sqrt{3}}{2}\)

Question 20.
The value of sin 3270°
(i) \(\frac{1}{\sqrt{2}}\)
(ii) \(\frac{1}{3}\)
(iii) \(\frac{1}{2}\)
(iv) \(\frac{\sqrt{3}}{2}\)
Answer:
(iii) \(\frac{1}{2}\)

Question 21.
The value of cos 2940° is :
(i) \(\frac{1}{\sqrt{3}}\)
(ii) \(\frac{1}{2}\)
(iii) \(\frac{1}{3}\)
(iv) \(\frac{\sqrt{3}}{2}\)
Answer:
(ii) \(\frac{1}{2}\)

Question 22.
The value of cos² 61° + cos² 29° will
(i) 0
(ii) 1
(iii) -1
(iv) 2
Answer:
(ii) 1

Question 23.
If sin θ = \(\frac{\sqrt{3}}{2}\) and 0° < θ < 90°, then the value of tan 2θ will be :
(i) -√3
(ii) –\(\frac{1}{\sqrt{3}}\)
(iii) \(\frac{1}{\sqrt{3}}\)
(iv) √3
Answer:
(i) -√3

Question 24.
The value of cos 2A is :
(i) cos² A – sin²A
(ii) 1 – 2 cos²A
(iii) cos²A + sin²A
(iv) 2 sin² A – 1.
Answer:
(i) cos² A – sin²A

Question 25.
The palue of sin 2A is :
(i) \(\frac{1+\tan ^{2} \mathrm{A}}{1-\tan ^{2} \mathrm{A}}\)
(ii) \(\frac{1-\tan ^{2} \mathrm{A}}{1+\tan ^{2} \mathrm{A}}\)
(iii) \(\frac{2 \tan \mathrm{A}}{1-\tan ^{2} \mathrm{A}}\)
(iv) \(\frac{2 \tan \mathrm{A}}{1+\tan ^{2} \mathrm{A}}\)
Answer:
(iv) \(\frac{2 \tan \mathrm{A}}{1+\tan ^{2} \mathrm{A}}\)

Question 26.
The value of cos (-405°) is :
(i) –\(\frac{1}{\sqrt{2}}\)
(ii) \(\frac{1}{\sqrt{2}}\)
(iii) \(\frac{1}{2}\)
(iv) –\(\frac{1}{2}\)
Answer:
(ii) \(\frac{1}{\sqrt{2}}\)

Question 27.
If sin θ = \(\frac{\sqrt{3}}{2}\) and 0° < θ < 90°, the value of cot 2θ will be :
(i) –\(\frac{1}{\sqrt{3}}\)
(ii) -√3
(iii) \(\frac{1}{\sqrt{3}}\)
(iv) √3
Answer:
(i) –\(\frac{1}{\sqrt{3}}\)

Question 28.
The value will be :
(i) -1
(ii) 0
(iii) 1
(iv) 3
Answer:
(i) -1

Question 29.
The value will be :
(i) -∞
(ii) -1
(iii) +1
(iv) ∞
Answer:
(ii) -1

Question 30.
The value of sec 70° sin 20° – cos 20° . cosec 70° will be :
(i) -1
(ii) 0
(iii) 1
(iv) infinity.
Answer:
(ii) 0

Question 31.
The value of sin 12° cos 78° + sin 78° cos 12° will be:
(i) 2
(ii) 1
(iii) 0
(iv) -1.
Answer:
(ii) 1

Question 32.
The maximum value of sin x for the value of x is :
(i) x = \(\frac{\pi}{4}\)
(ii) x = \(\frac{\pi}{2}\)
(iii) x = π
(iv) x = \(\frac{3 \pi}{2}\)
Answer:
(ii) x = \(\frac{\pi}{2}\)

Question 33.
Value of \(\frac{\sin 31^{\circ}}{\cos 59^{\circ}}\) will be :
(i) -1
(ii) 0
(iii) 1
(iv) 2.
Answer:
(iii) 1

Question 34.
If cosθ = \(\frac{1}{2}\), the value of cosec²θ is :
(i) \(\frac{1}{2}\)
(ii) \(\frac{\sqrt{3}}{2}\)
(iii) \(\frac{3}{4}\)
(iv) \(\frac{4}{3}\)
Answer:
(iv) \(\frac{4}{3}\)

Question 35.
The value of sec θ cosec θ tan θ is :
(i) sec²θ
(ii) cosec²θ
(iii) cos²θ
(iv) cosθ.
Answer:
(i) sec²θ

Question 36.
The value of cos 240° is :
(i) –\(\frac{\sqrt{3}}{2}\)
(ii) –\(\frac{1}{2}\)
(iii) \(\frac{1}{2}\)
(iv) \(\frac{\sqrt{3}}{2}\)
Answer:
(ii) –\(\frac{1}{2}\)

Question 37.
The value of \(\frac{2 \tan 15^{\circ}}{1+\tan ^{2} 15^{\circ}}\) is :
(i) \(\frac{\sqrt{3}}{2}\)
(ii) \(\frac{1}{\sqrt{2}}\)
(iii) \(\frac{1}{2}\)
(iv) \(\frac{1}{\sqrt{3}}\)
Answer:
(iii) \(\frac{1}{2}\)

Question 38.
The value of  is :
(i) \(\frac{1}{2}\)
(ii) \(\frac{\sqrt{3}}{2}\)
(iii) \(\frac{2}{\sqrt{3}}\)
(iv) \(\frac{\sqrt{2}}{1}\)
Answer:
(iii) \(\frac{2}{\sqrt{3}}\)

Question 39.
The value of sin (-300°) will be :
(i) \(\frac{\sqrt{3}}{2}\)
(ii) –\(\frac{\sqrt{3}}{2}\)
(iii) \(\frac{1}{2}\)
(iv) –\(\frac{1}{2}\)
Answer:
(i) \(\frac{\sqrt{3}}{2}\)

Question 40.
The value of sin (-1080°) will be:
(i) -1
(ii) 0
(iii) 1
(iv) ∞
Answer:
(ii) 0

Question 41.
The measure of the angle subtended at the centre of a circle of radius 10 min radian by the arc of measure 5π m will be :
(i) \(\frac{\pi}{2}\)
(ii) \(\frac{\pi}{4}\)
(iii) \(\frac{\pi}{5}\)
(iv) \(\frac{\pi}{10}\)
Answer:
(i) \(\frac{\pi}{2}\)

Question 42.
If tan α = sin α, then the value of α will be:
(i) 90°
(ii) 60°
(iii) 45°
(iv) 0°
Answer:
(iv) 0°

Question 43.
The value of 9 sec² θ – 9 tan² θ is :
(i) 1
(ii) 8
(iii) 9
(iv) 10
Answer:
(iii) 9
Solution.
9 sec² θ – 9 tan² θ = 9 ( sec² θ – tan² θ ) = 9 × 1 = 9
Hence, choice (iii) is correct

Question 44.
It tan θ = \(\frac{a}{b}\), then the value of \(\frac{b \sin \theta-a \cos \theta}{b \sin \theta+a \cos \theta}\) will be :
(i) 1
(ii) \(\frac{a^{2}-b^{2}}{a^{2}+b^{2}}\)
(iii) \(\frac{b^{2}-a^{2}}{b^{2}+a^{2}}\)
(iv) 0
Answer:
(iv) 0

Question 45.
The value of \(\frac{2 \tan 30^{\circ}}{1-\tan ^{2} 30}\) will be
(i) cos 60°
(ii) sin 60°
(iii) tan 60°
(iv) cot 60°
Answer:
(iii) tan 60°
Solution.

= √3 = tan 60°
Hence choice (iii) is correct. (iii)

Introduction to Trigonometry Class 10 Extra Questions Very Short Answer Type

Question 1.
Find the value of tan \(\left(\frac{11 \pi}{6}\right)\) :
Solution :
tan \(\left(\frac{11 \times 180}{6}\right)\)
= tan (11 × 30)
= tan 330°
= tan (360° – 30°)
= tan 30°
= – \(\frac{1}{\sqrt{3}}\)

Question 2.
If 3x₁ = cosec θ and \(\frac{3}{x_{2}}\) = cot θ find the value of
Solution.
Given, 3x₁ = cosec θ
∴ x₁ = \(\frac{1}{3}\) cosec θ

Question 3.
Prove that

Solution.

Question 4.
Find the value of \(\frac{\sin 27^{\circ}}{\cos 63^{\circ}}\).
Solution.

Question 5.
If cos A = \(\frac{\sqrt{3}}{2}\) , then find the value of sin 2A.
Solution.
Given, cos A = \(\frac{\sqrt{3}}{2}\) = cos 30°
∴ A = 30°
sin 2A = sin 2 × 30° = sin 60° = \(\frac{\sqrt{3}}{2}\)

Question 6.
If tan 2A = cot (A – 18°), where 2A is an acute angle find the value of A.
Solution.
tan 2A = cot (A – 18°)
⇒ cot (90° – 2A) = cot (A – 18°) [as cot (90 – θ) = tan θ]
⇒ 90° – 2A = A – 18°
⇒ 3A = 90° + 18° = 108°
∴ A = \(\frac{108}{3}\) = 36°

Question 7.
Solve the equation

Solution.

∴ θ = 60°

Question 8.
Prove that sin⁴ θ – cos⁴ θ = 2 sin² θ – 1.
Solution.
L.H.S. = sin⁴ θ – cos⁴ θ
= (sin² θ)² – (cos² θ)²
= (sin² θ + cos² θ) (sin² – cos² θ)
= 1[sin² – (1 – sin a )]
= 2 sin² θ – 1 = R.H.S.

Question 9.
If cosec A = 2, Find the value of
Solution.
Given, cosec A = 2 = cosec 30°
∴ A = 30° sin A


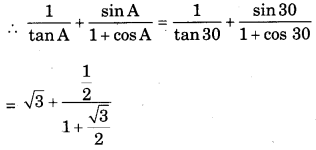
= √3 + 2 – √3
= 2

Question 10.
In ∆ABC, Prove :

Solution.
In ∆ABC
A + B + C = 180°(angle sum property of ∆)
= A + B = 180° – C

[∴ cos (90° – θ) = sin θ]

Question 11.
In a right ∆ABC, right angled at point C. If tan A = 1 prove that 2 sin A cos A = 1.

Solution.
tan A = 1 = \(\frac{BC}{CA}\)
∴ CA = BC = x (let)
By pythagoras theorem
BA² = BC² + CA²
= x² + x² = 2x²
∴ BA = x √2

∴ L.H.S. = 2. sin A cos A
= 2.\(\frac{1}{\sqrt{2}}\) × \(\frac{1}{\sqrt{2}}\)
= 1 = R.H.S

Question 12.
Prove


Solution.
(i) R.H.S. = (sec θ – tan θ)²

(ii) R.H.S. (cosec θ + cot θ)²

Question 13.
Prove (1 – sin θ) (1 + sin θ) (1 + tan² θ) = 1
Solution.
L.H.S. = (1 – sin θ) (1 + sin θ) (1 + tan² θ)
= (1 – sin² θ) (sec² θ)
[∵ 1 – sin² = cos² θ, 1 + tan² θ = sec² θ]
= cos² θ × sec² θ
= cos²θ × \(\frac{1}{\cos ^{2} \theta}\)
= 1 = R.H.S.

Question 14.
Prove : (1 + cot θ + tan θ) (sin θ – cos θ)
=
Solution.
L.H.S. = (1 + cot θ +, tan θ) (sin θ – cos θ)

Question 15.
Prove that:
cot A – cot 2A = cosec 2A.
Solution :
L.H.S. = cot A – cot 2A

= cosec 2A = R.H.S.

Question 16.
Find the value of :
(i) Find the value of top \(\frac{13 \pi}{6}\)
(ii) Find the value of sec \(\frac{23 \pi}{4}\)
(iii) Find the value of cot \(\frac{13 \pi}{3}\)
(iv) Find the value of (cos 75° + cos 15°).
Solution.

Question 17.
Prove that :

Solution :
L. H. S.

= R.H.S.

Question 18.
If cos (-840°) = –\(\frac{1}{2}\) then find the value of sin (-840°).
Solution.
cos (- 840°) = cos (840°)
= cos (120°) = –\(\frac{1}{2}\)
Hence
sin (-840°) = – sin 120° = \(\frac{-\sqrt{3}}{2}\)

Question 19.
If sin θ = \(\frac{4}{5}\), then find the value of cos 2θ.
Solution.
sin θ = \(\frac{4}{5}\)
cos 2θ = 1 – 2 sin²θ
= 1 – 2(\(\frac{4}{5}\))² = –\(\frac{7}{25}\)

Question 20.
Find the value of tan 35° tan 40° tan 45° tan 50° tan 55°
Solution.
tan 35o tan 40° tan 45o tan 50° tan 55°
= tan (90° – 55°) tan (90° – 50°) .1.tan 50° tan 55°
= cot 55° cot 50°.1.tan 50° tan 55°
= 1.

Question 21.
Prove that :

Solution :
R. H. S.

Question 22.
Prove.

Solution.
L. H. S.

Question 23.
Prove that : (cos A + cos B)² + (sin A + sin B)²

Solution :
L.H.S.
cos² A + cos² B + 2 cos A cos B
+ sin² A + sin² B + 2 sinA sinB
⇒ 1 + 1 + 2 (cos A cos B + sin A sin B)
⇒ 2 + 2 cos (A – B)
⇒ 2 [1 + cos (A – B)]

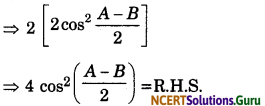
Question 24.
Prove the following:
(i)
(ii)
(iii)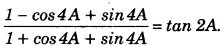
(iv) Find the value of

(v) Find the value of

(vi) Find the value of sin 3A in terms of sin A. Hence find the value of sin 135°. If A = 45°.
(vii) If sin θ = \(\frac{3}{25}\), find the value of sin 2θ
Solution.
(i)

(ii)

(iii)

(iv)

(v)

(vi) sin 3A = sin(2A + A)
= sin 2A. cos A + cos 2A.sin A
= 2sin A.cos A. cos A + (1 – 2 sin²A).sin A
= 2 sin A(1 – sin²A) + sin A – 2 sin³A
= 2 sin A – 2 sin³A + sin A – 2 sin³A
= 3 sin A – 4 sin³A.
∴ sin 135° = sin(3 × 45°)
= 3 sin 45° – 4 sin³ 45°

(vii) As sin 2 θ = 2 sin θ . cos θ

Question 25.
Prove that : sec θ (1 – sin θ) (sec θ + tan θ) = 1
Solution :
L.H.S.

Question 26.
Prove that :
cos 33°cos 27 – cos 57°cos 63° = \(\frac{1}{2}\)
Solution :
L.H.S.
cos 33° cos 27° – cos (90°-33°) cos (90° – 27°)
∴ cos 33° cos 27° – sin 33° sin27°
∴ cos (33° + 27°) = cos (60°)
= \(\frac{1}{2}\)

Question 27.
Find the value of :
cos 80o.cos 70° – cos 10° cos 20°.
Solution.
cos 80° cos 70° – cos 10° cos 20°
= cos(90° – 10°) cos(90° – 20°) – cos 10° cos 20°
= sin 10° sin 20° – cos 10° cos 20°
= – (cos 10° cos 20° – sin 10° sin 20°)
= -cos(10° + 20°)
= -cos 30° = –\(\frac{-\sqrt{3}}{2}\).

Question 28.
Prove :

Solution.

L.H.S. sin 5A – 2 sin 3A + sin A cos 5A – 2 cos 3A + cos A
sin 5A +sin A – 2 sin 3A , cos 5A + cos A – 2 cos 3A
2sin 3A cos 2A – 2sin 3A 2 cos 3A cos 2A – 2 cos 3A 2sin 3A(cos 2A – 1)
2cos 3A (cos 2A – 1) = tan 3A = R.H.S.

Question 29.
Prove cos² π/8 + cos²3π + cos² 5π/8 + cos² 7π/8 = 2.
Solution :

1 + 1 = 2 = R.H.S.

Question 30.
Prove :
cos 4A = 1 – 8 sin²A + 8 sin⁴A
Solution :
L. H. S.
cos 4A = cos 2(2A)
= 1 – 2 sinθ 2A
= 1 – 2 (2 sin A cosA)²
= 1 – 8 sin² A cos²A
= 1 – 8 sin – A (1 – sin² A)
= 1 – 8 sin² A + 8 sin⁴A
= R.H.S.

Introduction to Trigonometry Class 10 Extra Questions Short Answer Type

Question 1.
Prove that :

Solution :
L.H.S.

= 1 + 1 = 2 = R.H.S.

Question 2.
Prove that:

Solution :
L. H. S.

= 2 × cosec A = R.H.S.

Question 3.
Prove that :
\(\frac{\sin 8 A}{\sin A}\) = 8 cos A cos 2A cos 4A
Solution :

= 8 cos A cos 2A cos 4A = R.H.S

Question 4.
Prove that : (1 – sin θ)(1 + sin θ)( 1+ tan2θ)= 1
Solution :
L.H.S.
= (1- sin A)(1 + sin )( 1+ tan2θ)
= (1 – sin² θ) × sec²θ
= cos²θ × \(\frac{1}{\cos ^{2} \theta}\) = 1
= R.H.S.

Question 5.
Prove that : sin A (1 + tan A) + cos A (1 + cot A) = sec A + cosec A
Solution.

= sec A + cosec A R.H.S.

Question 6.
Find the value of

Solution :
(cos 15° + sin 15°)

Question 7.
Prove that : 16 cos 20° cos 40° cos 60° cos 80° = 1
Solution:
L.H.S.= 16 cos 20° cos 40° cos 60° cos 80°
= 8 × \(\frac{1}{2}\) (2 cos 80° cos 40°) cos 20°
= 4 (cos 120° cos 40°) cos 200 = 2. 2. – cos 20° + cos 40ocos 2007
= 2 [-cos 20° + cos 60° + cos 20°]
= 2 × \(\frac{1}{2}\) = 1 = R.H.S.

Question 8.
Prove that:

Solution :
L.H.S.
= sec²A – sec²A – tan²A × tan²A
= sec⁴ A – tan⁴A
= (sec²A -tan²A)(sec²A + tan²A)
= 1 (1 + tan²A + tan²A)
= 1 + 2 tan2A = R.H.S.

Question 9.
Prove that :

Solution :
L.H.S. =

= 2 cot θ = R.H.S.

Question 10.
Prove that :
(i) If 2 tan P= 3 tan Q, then prove that:
tan(P – Q) = \(\frac{\sin 2 Q}{5-\cos 2 Q}\)
(ii) If cos A + sin A = √2 cos A, prove that cos A – sin A = √2 sin A . sin 63° + cos 630

Solution.

(ii) Given cos A + sin A = √2cos A
∴ sin A = (√2 – 1) cos A Now, multiply both sides by (√2 +1)
∴ (√2 + 1)sin A = (√2 + 1) (√2 – 1) cosA
= √2 sin A + sin A = cos A
Hence, √2sin A = cos A – sin A.

(iii)

(iv) L.H.S.

Question 11.
If cosec A = \(\frac{17}{15}\), then find the value of sec A.
Solution.
cosec A = \(\frac{17}{15}\)
sin A = \(\frac{15}{17}\)
cos A = \(\frac{8}{17}\)
∵ sec A = \(\frac{17}{8}\)

Question 12.
Prove that

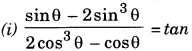
(i) θ, (ii) cos² θ + cos² θ.cot² θ = cot² θ
Solution.

(ii) L.H.S. = cos² θ + cos² x cot² θ
= cos² θ[1 + cot² θ]
= cos² θ × cosec²θ
= cos θ × \(\frac{1}{\sin ^{2} \theta}\) = cot² θ = R.H.S.

Question 13.
Solve the equation :

Solution.

Question 14.
If (A + B) = 45°, then prove that (1 + tan A) (1 + tan B) = 2
Solution.
A + B = 45°
⇒ tan(A + B) = tan 45o
⇒ \(\frac{\tan A+\tan B}{1-\tan A \tan B}\) = 1
⇒ tan A + tan B = 1 – tan A tan B
⇒ tan A + tan B + tan A tan B = 1
⇒ 1 + tan A + tan B + tan A tan B = 1 + 1
(1 + tan A) + tan B(1 + tan A) = 2
(1 + tan A)(1+tan B) = 2

Question 15.
Prove that tan 75° = 2 + √3.
Solution.
tan 75°
= tan (45° + 30°)

Question 16.
Prove that

Solution.

Question 17.
Find the value of \(\frac{\sin 65^{\circ}}{\sin 115^{\circ}}\)
Solution.
We have,

Question 18.
Prove that

Solution.

Question 19.
Prove that sec 70° sin 20° + cos 20° cosec 70° = 2
Solution.
L. H. S.
sec 70° sin 20° + cos 20° cosec 70°

Question 20.
Prove that :
(i) cos 2A = \(\frac{1-\tan ^{2} A}{1+\tan ^{2} A}\)
(ii)
Solution.
(i) R.H.S

(ii)

Question 21.
If sec θ + tan θ = p, prove that
\(\frac{p^{2}-1}{p^{2}+1}\) = sin θ.
Solution.

Question 22.
If A = 30° and B = 60°, then prove that sin(A + B) = sin A cos B + cos A sin B.
Solution.
L.H.S. = sin (A + B)
= sin (30° + 60°)
= sin 90° = 1
R.H.S. = sin A cos B + cos A sin B
= sin 30°. cos 60° + cos 30°.sin 60°

L.H.S. = R.H.S.

Question 23.
Find the value of sin 65o cos 35° – cos 65° sin 35°.
Solution.
sin 65° cos 35° – cos 65° sin 35°
= sin(65° – 35°)
= sin 30° = \(\frac{1}{2}\)

Question 24.
If sinθ = \(\frac{9}{41}\), then find the value of tan θ – cosec θ.
Solution.

Question 25.
Find the value of sin A cos(90° – A) + cos A sin(90° – A).
Solution.
sin A cos (90° – A) + cos A sin (90° – A)
= sin A sin A + cos A cos A
= sin²A + cos²A = 1

Question 26.
Prove that :
\(\sqrt{\frac{1-\cos \theta}{1+\cos \theta}}\) = cosec θ – cot θ
Solution.

cosec θ – cot θ = R.H.S.

Question 27.
(a) Prove that :

Or
sin 4θ – cos 4θ = 2 tan²θ – 1.
(b) Prove that :
cos⁴θ – sin²θ = cos 2θ.
(c) Find the value of cos 375°.
Solution.
(a) Do yourself.
(b) Do yourself.
(c) cos 375° = cos (360° + 15°)
= cos 15o = cos (45° – 30°)
= cos 45°.cos 30° + sin 45o.sin 30°

Question 28.
Prove that: sin 3A cos3A + cos 3A. sinA = \(\frac{3}{4}\) sin 4A.
Solution.
Do yourself.

Question 29.
Prove that :

Solution.
Do yourself.

Question 30.
(a) Prove that:

Solution.

Question 31.
Prove :
\(\frac{\sec A-\tan A}{\sec A+\tan A}\)
= 1 – 2 sec A tan A + 2 tan²A
Solution.
L.H.S. – \(\frac{\sec A-\tan A}{\sec A+\tan A}\)

= 1 + tan²A + tan² – A – 2sec A tan A
= 1 – 2 sec A. tan A + 2 tan²A
= R.H.S.

Question 32.
Prove :
2cos A + cos 3A + cos 5A
= 4 cos A cos² 2A.
Solution.
L.H.S. = 2 cos A + cos 3A + cos 5A
= 2 cos A + 2 cos 4A cos (-A)
= 2 cos A + 2 cos 4A cos A
= 2 cos A(1 + cos 4A)
= 2 cos A(1 + 2 cos²2A – 1)
= 4 cos A cos²2A = R.H.S.

Question 33.
Prove : sin²A – sin²B = sin(A + B) sin(A – B).
Solution.
L.H.S. = sin²A – sin²B
= (sin A – sin B) (sin A + sin B)

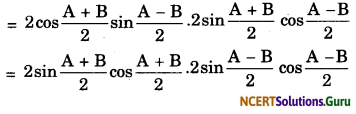
= sin(A + B).sin(A – B)
= R.H.S.

Question 34.
Prove :

Solution.
L.H.S.


L.H.S. = R.H.S.

Question 35.
Prove :
Proved.
sec A – tan A = \(\frac{1}{\sec A+\tan A}\)
Solution.
L.H.S. = sec A – tan A

So, L.H.S. = R.H.S.

Question 36.
Prove that :

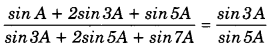
Solution.
L.H.S.

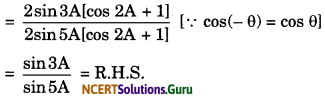
Introduction to Trigonometry Class 10 Extra Questions Long Answer Type

Question 1.
Prove that:
(cos A + cos B)² + (sin A – sin B)²
= 4 cos² \(\left(\frac{A+B}{2}\right)\)
Solution.
L.H.S.
cos²A + cos²B + 2cos A cos B + sin²A
+ sin²B – 2 sin A sinB
⇒ (cosA + sinoA) + (cos’B + sino B)
+ 2 (cosA cos B – sin A sin B)
⇒ 1 + 1 + 2 cos (A – B)
⇒ 2[1 + cos (A – B)]

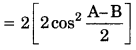
= 4cos² \(\frac{A-B}{2}\)
= R.H.S.

Question 2.
Prove that:
\(\sqrt{\frac{1-\sin A}{1+\sin A}}\)= sec A – tan A
Solution.

= sec A – tan A
= R.H.S.

Question 3.
Prove that :

Solution :
L.H.S.


= sec A- sec A + tan A
= tan A ……(ii)
From (i) and (ii)
L.H.S. = R.H.S.

Question 4.
Prove that : cos³A cos3A + sin³A sin3A = cos³2A.
Solution :

= cos³ 2A = R.H.S.

Question 5.
If \(\frac{\cos \alpha}{\cos \beta}\) = n, \(\frac{\sin \alpha}{\sin \beta}\) = m prove that
(m² – n²) sin²β = 1 – n².
Solution.
cos α = n cos β and sin α = m sin β
Squaring and adding we get
cos²α + sin² α = n² cos²β + m² sin² β.
⇒ 1 = n² (1 – sin²β) + m² sin² β
⇒ 1 = n² – n² sin² β + m2 sino β
⇒ 1 – n² = sin²β (m² – n²)

Question 6.
Prove that :
sin 20° sin 40° sin 80° = \(\sqrt{\frac{3}{8}}\)
Solution :

Question 7.
Prove :

Solution :

Question 8.
Prove :

Solution.
L.H.S.

= (cosec θ + cot θ)² = R.H.S. Proved

Question 9.
Prove:
tan² θ + cot² θ + 2 = sec² θ.cosec² θ
Solution.
tan²θ + cot² θ + 2
= (1 + tan²θ) + (1 + cot²θ)
= sec² θ + cosec² θ

= sec² θ cosec² θ = R.H.S.

Question 10.
If A + B + C = 180°, Prove that :
(i) sin A + sin B + sin C = 4 cos\(\frac{A}{2}\) . cos\(\frac{B}{2}\) . cos\(\frac{C}{2}\)
(ii) cot A . cot B + cot B . cot C + cot C . cot A = 1
(iii) sin 2A + sin 2B + sin 2C = 4 sin A sin B . sin C
(iv) cos A + cos B + cos C = 1 + 4 sin\(\frac{A}{2}\) . sin\(\frac{B}{2}\) . sin\(\frac{C}{2}\)
(v) sin A + sin B – sin C = 4 sin\(\frac{A}{2}\) . sin\(\frac{B}{2}\) . cos\(\frac{C}{2}\)
(vi) Prove :

Solution.
(i) L.H.S.
= sin A + sin B + sin C

(ii) We have,
A + B + C = 180°
⇒ A + B = 180°- C
∴ cot(A + B) = cot(180° – C)
⇒ \(\frac{\cot A \cdot \cot B-1}{\cot B+\cot A}\) = -cot C
⇒ cot A . cot B – 1 = -cot B . cot C – cot A . cot C
⇒ cot A . cot B + cot B . cot C + cot C . cot A = 1
= R.H.S.

(iii) L.H.S. = sin 2A + sin 2B + sin 2C

= 2 sin(A + B) . cos(A – B) + 2 sin C.cos C…(i)
∵ A+B+C = 180°
∴ A + B = 180° – C
⇒ sin(A + B) = sin(180° – C)
= sin C
and cos (A + B) = cos (180° – C)
= -cos C
Putting value in (i),
= 2 sin C.cos(A – B) – 2 sin C. cos(A + B)
= 2 sin C[cos (A – B) – cos(A + B)]

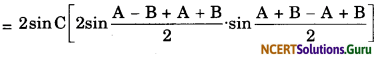
= 2 sin C(2 sin A.sin B]
= 4 sin A . sin B . sin C
= R.H.S.

(iv) L.H.S. = cos A + cos B + cos C

= R.H.S.

(v) Do yourself.

(vi) L.H.S.

Question 11.
Prove that:

= cos 2θ – tan 3θ . sin 2θ.
(ii) sin 10° . sin 30° . sin 50° . sin 70° = \(\frac{1}{16}\)
(iii) cos 20° . cos 40° cos 60°. cos 80° = \(\frac{1}{16}\)
(iv)
(v) sin 20°.sin 40° sin 60°.sin 80° = \(\frac{3}{16}\)
(vi) tan 70° = tan 20° + 2 tan 50°.
(vii) tan 3A – tan 2A – tan A = tan 3A . tan 2A tan A.
(viii) If A + B + C = 90°, prove that
tan A tan B + tan B tan C + tan C tan A = 1
(ix) Prove that :

(x) Prove :

+ (sin A + sin B)²
Solution.
(i) L.H.S.

= cos 2θ – tan 3θ.sin 2θ
= R.H.S.

(ii) L.H.S. = sin 10° sin 50° sin 70° sin 30°

(iii) L.H.S. = cos 20° cos 40°.cos 80°.cos 60°

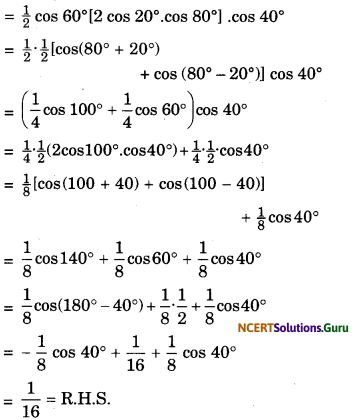
(iv)

(v) L.H.S.
= sin 20° sin 40° sin 60° sin 80°
= sin 60° sin 20° sin 40° sin 80°

L.H.S. = R.H.S.

(vi) tan 70° = tan(50° + 20°) .

⇒ tan 70° – tan 70° tan 50° tan 20°
= tan 50° + tan 20°
⇒ tan 70° – tan(90° – 20°) tan 50°
tan 20° = tan 50° + tan 20°
⇒ tan 70° – cot 20° tan 50° tan 20°
= tan 50° + tan 20°
⇒ tan 70° – \(\frac{1}{\tan 20^{\circ}}\) tan 50° tan 20°
= tan 50° + tan 20°
⇒ tan 70° – tan 50° = tan 50° + tan 20°
⇒ tan 70° = tan 50° + tan 20°+ tan 50°
⇒ tan 70°= tan 20° + 2tan 50°

(vii) We have
tan 3A = tan(A + 2A)
tan A + tan 2A
⇒ tan 3A = \(\frac{\tan A+\tan 2 A}{1-\tan A \tan 2 A}\)
⇒ tan 3A – tan 3A tan A tan 2A = tan A + tan 2A
⇒ tan 3A – tan 2A – tan A
= tan 3A tan 2A tan A.

(viii) Given
A + B + C = 90°
⇒ A + B = 90° – C
⇒ tan(A + B) = tan(90° – C)
⇒ \(\frac{\tan A+\tan B}{1-\tan A \tan B}\) = cot C = \(\frac{1}{\tan C}\)
⇒ tan =tan A . tan C + tan B . tan C
= 1 – tan A tan B
⇒ tan A tan B + tan B . tan C + tan C . tan A = 1

(ix)


= sec A + tan A
= R.H.S.

(x) R.H.S. = (cos A-cos B)² + (sin A + sin B)²
= cos²A + cos²B – 2cos A cos B
+ sin²A + sin²B + 2 sin A sin B
= (cos² A +sin² A) + (cos²B + sin²B)
– 2{cos A cos B – sin A sin B]
= 1 + 1 – 2[cos A.cos B – sin A.sin B]
= 2[1 – cos(A + B)]

= L.H.S.

Question 12.
Solve :

Solution.

⇒ cos θ = cos 60°
∴ θ = 60°

Question 13.
Prove : (cos A + sec A)² + (sin A + cosec A)² 7 + tan² A + cot² A.
Solution.
L.H.S.
= (cos A + sec A)² + (sin A + cosec A)²
= cos²A + sec²A + 2.cos A sec A + sin² A + cosec²A + 2sin A cosec A
= 1 + 2 + 2 + sec²A + cosec² A
= 5 + 1 + tan²A + 1 + cot² A
= 7 + tan²A + cot²A
= R.H.S.

Question 14.
Prove :

Solution :

Question 15.
Prove that:
tan (A + B) tan (A – B)

Solution.
tan (A + B)

Question 16.

Solution.
L. H. S.


= tan 5 A = R.H.S.

Question 17.
Prove :
cos A cos (60° + A). Cos (60° – A) = \(\frac{1}{4}\) cos 3A
Solution.
L.H.S.
= cos A. cos (60° + A). cos (60° – A)
= cos A (cos 60°. cos A-sin 60° sin A)
(cos 60°. cos A + sin 60°sin A)

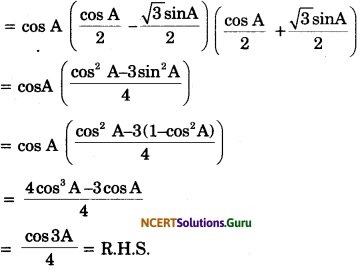
Question 18.
Prove :

Solution.
L.H.S.


= tan (A – B)
= R.H.S.

Question 19.
Prove :
sin A sin 2 A + sin 3A sin 6A = sin 4A sin 5A.
Solution.
L.H.S.
= sin A sin 2A + sin3 A sin 6A
= \(\frac{1}{2}\) [2 sin A sin 2A + 2 sin3A sin 6A]
= \(\frac{1}{2}\) [cos A – cos 3A + cos 3 A – cos 9A]
= \(\frac{1}{2}\) [cos A – cos 9A]
= \(\frac{1}{2}\) × 2 sin \(\frac{9 \mathrm{A}+\mathrm{A}}{2}\) sin \(\frac{9 \mathrm{A}-\mathrm{A}}{2}\)
= sin 5A sin 4A
= sin 4A sin 5A = R.H.S.

Question 20.
Prove :

Solution.
L.H.S.

= sec θ + tan θ = R.H.S.