Here you will find Pair of Linear Equations in Two Variables Class 10 Extra Questions Maths Chapter 3 with Answers Solutions, Extra Questions for Class 10 Maths are solved by experts and will guide students in the right direction.
Extra Questions for Class 10 Maths Pair of Linear Equations in Two Variables with Answers Solutions
Extra Questions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables with Solutions Answers
Pair of Linear Equations in Two Variables Class 10 Extra Questions Objective Type
Question 1.
If the pair of linear equations x – y – k = 0 and 6x – 2y – 3 = 0 represent an infinite solution, then the value of k is:
(a) k = 1
(b) k = 2
(c) k = 0
(d) No value of k
Answer:
(d) No value of k
Question 2.
If the pair of equations 6x + 5y = 4 and 12x + py = -8 has no solution, then the value of p is:
(a) 9
(b) 10
(c) 7
(d) 6
Answer:
(b) 10
![]()
Question 3.
The solution of the equation 2x + 3y = 18 and x – 2y = 2 is
(a) x = 2, y = 6
(b) x = 6, y = 2
(c) x = – 6, y = -2
(d) None of these
Answer:
(b) x = 6, y = 2
Question 4.
Find the values of x and y in the following equations:
x – 3y = 8 and 5x + 3y = 10
(a) x = 3, y = – \(\frac {5}{3}\)
(b) x = -3, y = \(\frac {5}{3}\)
(c) x = -3, y = – \(\frac {5}{3}\)
(d) None of these
Answer:
(a) x = 3, y = – \(\frac {5}{3}\)
Pair of Linear Equations in Two Variables Class 10 Extra Questions Very Short Answer Type
Question 1.
Solve the following pair of linear equations by the substitution method.
(i) x + y = 14, x – y = 4
(ii) 3x – y = 3, 9x – 3y = 9
(iii) √2x + √3y = 0, √3x – √8y = 0
Solution:
(i) We have,
x + y = 14 …..(i)
and x – y = 4 ……(ii)
From Eq. (ii), y = x – 4 …(iii)
Substituting y from Eq. (iii) in Eq. (i), we get
x + x – 4 = 14
⇒ 2x = 18.
⇒ x = 9
On substituting x = 9 in Eq. (iii), we get
y = 9 – 4 = 5
⇒ y = 5
x = 9, y = 5
(ii) We have,
3x – y = 3 …(i)
and 9x – 3y = 9 …(ii)
From Eq. (i)y = 3x – 3 …. (iii)
On substituting y from Eq. (iii) in Eq. (ii), we get
9x – 3(3x – 3) = 9
⇒ 9 = 9
It is a true statement. Hence, every solution of Eq. (i) is a solution of Eq. (ii) and vice-versa.
On putting x = k in Eq. (i), we get
3k – y = 3 ⇒ y = 3k – 3
∴ x = k, y = 3k – 3 is a solution for every real k.
Hence, infinitely many solutions exist.
(iii) We have,
√2x + √3y = 0 …..(i)
and √3x – √8y = 0 …(ii)
From Eq. (ii),
√8y = √3x
⇒ y = \(\frac{\sqrt{3} x}{\sqrt{8}}\) …..(iii)
On substituting y from Eq. (iii) in Eq. (i), we get

⇒ √2 x √8x + 3x = 0
⇒ √16x + 3x = 0
⇒ 4x + 3x = 0
⇒ 7x = 0
⇒ x = 0
Putting x = 0 in Eq. (iii), y = 0
![]()
Question 2.
Form the pair of linear equations in the following problems and find their solutions (if they exist) by the elimination method
(i) If we add 1 to the numerator and subtract 1 from the denominator, a fraction reduces to 1. It becomes \(\frac {1}{2}\), if we only add 1 to the denominator. What is the fraction ?
(ii) Five years ago, Nuri was thrice as old as Sonu. Ten years later, Nuri will be twice as old as Sonu. How old are Nuri and Sonu ?
Solution:
(i) Let the fraction be \(\frac {x}{y}\)
According to the given conditions,
![]()
⇒ x + 1 = y – 1; 2x = y + 1 ……..(i)
⇒ x – y = -2 and 2x – y = 1 ……..(ii)
On subtracting Eq. (i) from Eq. (ii),
(2x – y) – (x – y) = 1 + 2
⇒ x = 3
On substituting x = 3 in Eq. (i),
3 – y = -2 ⇒ y = 5
Hence, the fraction is \(\frac {3}{5}\)
(ii) Let present age of Nuri = x years. Present age of Sonu = y years
According to the given conditions,
Five years ago,
x – 5 = 3(y – 5)
⇒ x – 3y = -10 …(i)
Ten years later,
x + 10 = 2(y + 10)
⇒ x – 2y = 10 …(ii)
On subtracting Eq. (i) from Eq. (ii),
(x – 2y) – (x – 3y) = 10 + 10
⇒ – 2y + 3y = 20
⇒ y = 20
From Eq. (ii), substituting y = 20, we get
⇒ x = 2y + 10 = 2 × 20 + 10
⇒ x = 50
Therefore, present age of Nuri = 50 years and present age of Sonu = 20 years
![]()
Question 3.
For What value of k, will the pair of linear equations kx + y = k2 and x + ky = 1 have infinitely many solutions ?
Solution:
Given equation are
kx + y = k2 ……(i)
and x + ky = 1 ……(ii)
have infinitely many solution
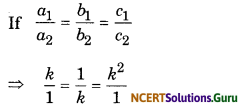
∴ k2 = 1 = k ⇒ ± 1
and k3 = 1 ⇒ k = 1
Hence k = 1
Pair of Linear Equations in Two Variables Class 10 Extra Questions Short Answer Type
Question 1.
Solve the following pairs of equations by reducing them to a pair of linear equations:
(i) \(\frac {4}{x}\) + 3y =14 and \(\frac {3}{x}\) – 4y = 23
(ii) 
![]()
Solution:
(i) We have,
\(\frac {4}{x}\) + 3y =14 and \(\frac {3}{x}\) – 4y = 23
On putting \(\frac {1}{x}\) = X, we get
4x + 3y = 14 …..(i)
and 3x – 4y = 23 … (ii)
On multiplying Eq. (i) by 4 and Eq. (ii) by 3 and then adding, we get
16X + 9X = 4 × 14 + 3 × 23
⇒ 25X = 56 + 69
⇒ 25X = 125 = X = 5
Then, \(\frac {1}{x}\) = 5
⇒ x = \(\frac {1}{5}\) From Eq. (i), substituting x = 5, we get
4 × 5 + 3y = 14 = 3y = 14 – 20
⇒ 3y = -6 = y = -2
Hence, x = and y = -2

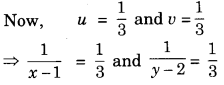
⇒ x – 1 = 3 and y – 2 = 3
⇒ x = 3 + 1
and y = 3 + 2
⇒ x = 4 and y = 5
![]()
Question 2.
Prove that the pair of linear equation \(\frac {22}{7}\)x + \(\frac {22}{7}\)y = 7 and y = 7 and 9x – 10y = 14 is coinsistent find its solution by method cross-multiplication.
Solution:
Given equation are
\(\frac {22}{7}\)x + \(\frac {22}{7}\)y = 7
⇒ 3x + 5y = 14 ….(i)
and 9x – 10y = 14 …(ii)
If \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\) then equation are coinsistance.
Here a1 = 3, b1 = 5, c1 = – 14
and a2 = 9, b2 = -10, c2 = -14

Question 3.
Solve the following pair of linear equations.

x ≠ 0, y ≠ 0
Solution:
Suppose \(\frac{1}{x-y}\) = a
and \(\frac{1}{x+y}\) = b
The reduced equation will be
15a + 22b = 5 ….(i)
and 40a + 55b = 13 (ii)
Multiply equation (i) by 8 and equation (ii) by 3, we get
120a + 176b = 40
and 120a + 165b = 39
on substracting 11b = 1

∴ x – y = 5 … (iv)
Solving Eq. (iii) and Eq. (iv) we get.
x = 8 and y = 3
![]()
Question 4.
The sum of a two-digit number and the number obtained by reversing the digits is 66. If the digits of the number differ by 2. Find the number.
Solution:
Let unit digit of the number bex and ten’s digit of the number be y
∴ Number = 10y + x
and Number obtain by reversing the digits is 10x + y
∴ By Ist condition,
(10y + x) + (10x + y) = 66
⇒ 11x + 11y = 66
∴ x + y = 6 ……(i)
By IInd condition, x – y = 2 (ii)
On adding (i) & (ii)
2x = 8
∴ x = 4
from equation (1), y = 6 – 4 = 2
Hence, required Number be 2 × 10 + 4 = 24
Pair of Linear Equations in Two Variables Class 10 Extra Questions Short Answer Type 2
Question 1.
7 chairs and 4 tables for a classroom cost ₹ 7000 while 5 chairs and 6 tables cost ₹ 5080. Find the cost of each chair and that of each table.
Solution:
Let the cost of each chair be ₹ x and that of each table be ₹ y.
Then,
7x + 4y = 7000 …(i)
5x + 3y = 5080 …(ii)
On multiplying (i) by 3, (ii) by 4 and subtracting, we get:
(21x – 20x) = (21000 – 20320)
⇒ x = 680.
On substituting x = 680 in (i), we get:
(7000 – 4760) 4y = 7000
⇒ 4y = (7000 – 4760)
⇒ y = 560.
∴ cost of each chair = ₹ 680 and cost of each table = ₹ 560.
![]()
Question 2.
The sum of a two-digit number and the number obtained by reversing the order of its digits is 99. If the digits differ by 3, find the number.
Solution:
Let the tens and units digits of the required number be x and y respectively.
Then, the number = (10x + y).
The number obtained on reversing the digits = (10y + x).
∴ (10y + x) + (10x + y) = 99
= 11(x + y) = 99
⇒ x + y = 9.
Also, (x – y) = ± 3.
∴ x + y = 9 …..(i)
x – y = 3 …..(ii)
x + y = 9 ….(iii)
x – y = -3 …..(iv)
From (i) and (ii), we get: x = 6, y = 3.
From (iii) and (iv), we get: x = 3, y = 6.
Hence, the required number is 63 or 36.
![]()
Question 3.
The monthly incomes of A and B are in the ratio 8 : 7 and their expenditures are in the ratio 19 : 16. If each saves ₹ 5000 per month, find the monthly income of each.
Solution:
Let the monthly incomes of A and B be ₹ 8x and ₹ 7x respectively, and let their expenditures be ₹ 19y and ₹ 16y respectively.
Then, A’s monthly savings = ₹ (8x – 19y).
And, B’s monthly savings = ₹ (7x – 16y).
But, the monthly saving of each is ₹ 5000.
∴ 8x – 19y = 5000 …..(i)
7x – 16y = 5000…..(ii)
Multiplying (ii) by 19, (i) by 16 and subtracting the results, we get:
(19 × 7 – 16 × 8)x = (19 × 5000 – 16 × 5000)
⇒ (133 – 128)x = (19 – 16) 5000
⇒ 5x = 15000
⇒ x = 3000.
∴ A’s monthly income = ₹ (8x) = ₹ (8 × 3000) = ₹ 24000.
And, B’s monthly income = ₹ (7x) = ₹(7 × 3000) = ₹ 21000.
![]()
Question 4.
A two-digit number is such that the product of its digits is 14. If 45 is added to the number, the digits interchange their places. Find the number.
Solution:
Let the tens and units digits of the required number be x and y respectively.
Then, xy = 14.
Required number= (10x + y).
Number obtained on reversing its digits = (10y + x).
∴ (10x + y) + 45 = (10y + x)
⇒ 9(y – x) = 45
⇒ y – x = 5 …(i)
Now, (y + x)2 – (y – x)2 = 4xy

= y + x = 9 …(ii)
[∴ digits are never negative)
2y = 14 ⇒ y = 7.
Putting y = 7 in (ii), we get:
7 + x = 9 ⇒ x = (9 – 7) = 2.
x = 2 and y = 7.
Hence, the required number is 27.
![]()
Question 5.
The sum of the numerator and the denominator of a fraction is 12. If the denominator is increased by 3, the fraction becomes \(\frac {1}{2}\). Find the fraction.
Solution:
Let the required fraction be \(\frac {x}{y}\).
Then,
∴ x + y = 12 ……(i)
and \(\frac{x}{y+3}\) = \(\frac{1}{2}\)
⇒ 2x = y + 3
⇒ 2x – y = 3 …(ii)
Adding (i) and (ii), we get:
3x = 15 x = 5.
Putting x = 5 in (i), we get:
5 + y = 12 y = (12 – 5) = 7.
Thus, x = 5 and y = 7.
Hence, the required fraction is \(\frac {5}{7}\).
![]()
Question 6.
Five year ago, A was thrice as old as B and ten years later A shall be twice as old as B. What are the present ages of A and B ?
Solution:
Let the present ages of B and A be x years and y years respectively. Then,
B’s age 5 years ago = (x – 5 ) years and A’s age 5 years ago = (y – 5) years.
∴ (y – 5) = 3(x – 5) = 3x – y = 10 …(i)
B’s age 10 years hence = (x + 10) years.
A’s age 10 years hence = (y + 10) years.
∴ (y + 10) = 2(x + 10) = 2x – y = -10 (ü)
On subtracting (ii) from (i), we get:
x = 20.
Putting x = 20 in (i), we get:
(3 x 20) – y = 10 = y = (60 – 10) = 50.
∴ x = 20 and y = 50.
Hence, B’s present age = 20 years and A’s present age = 50 years.
![]()
Question 7.
If the length of a rectangle is reduced by 5 units and its breadth is increased by 2 units, then the area of the rectangle is reduced by 80 sq units. However, if we increase its length by 10 units and decrease the breadth by 5 units, its area is increased by 50 sq units. Find the length and breadth of the rectangle.
Solution:
Let the length and breadth of the rectangle be x units and y units respectively.
Then, area of the rectangle = xy sq units
Case I: When the length is reduced by 5 units and the breadth is increased by 2 units.
Then,new length= (x – 5) units
andnew breadth = (y + 2) units.
∴ new area = (x – 5)(y + 2) sq units.
∴ xy – (x – 5)(y + 2) = 80
⇒ 5y – 2x = 70…(i)
Case II: When the length is increased by 10 units and the breadth is decreased by 5 units.
Then, new length= (x + 10) units
andnew breadth = (y – 5) units.
∴ new area = (x + 10)(y – 5) sq units.
∴ (x + 10)(y – 5) – xy = 50
⇒ 10y – 5x = 100
⇒ 2y – x = 20 …….(ii)
On multiplying (ii) by 2 and subtracting esult from (i), we get:
y = 30.
Putting y = 30 in (ii), we get:
(2 × 30) – x = 20 ⇒ 60 – x = 20
⇒ x = (60 – 20) = 40.
∴ x = 40 and y = 30.
Hence, length = 40 units and breadth = 30 units.
![]()
Question 8.
8 men and 12 boys can finish a piece of work in 5 days, while 6 men and 8 boys can finish it in 7 days. Find the time taken by 1 man alone and that by 1 boy alone to finish the work…
Solution:
Suppose 1 man alone can finish the work in x days and 1 boy alone can finish it in y days.
Then, 1 man’s 1 day’s work = \(\frac {1}{x}\)
And, 1 boy’s 1 day’s work = \(\frac {1}{y}\)
8 men and 12 boys can finish the work in 5 days
⇒ (8 men’s 1 day’s work) + (12 boys’ 1 day’s work) = \(\frac {1}{5}\)
⇒ \(\frac {8}{x}\) + \(\frac {12}{y}\) = \(\frac {1}{5}\),
⇒ 8υ + 12υ = \(\frac {1}{5}\),
[Where \(\frac {1}{x}\) = υ and \(\frac {1}{y}\) = υ] …..(i)
Again, 6 men and 8 boys can finish the work in 7 days
⇒ (6 men’s 1 day’s work) + (8 boys’ 1 day’s work) = \(\frac {1}{7}\)

∴ one man alone can finish the work in 70 days,
and one boy alone can finish the work in 140 days.
![]()
Question 9.
A boat goes 16 km upstream and 24 km downstream in 6 hours. Also, it covers 12 km upstream and 36 km downstream at the same time. Find the speed of the boat in still water and that of the stream.
Solution:
Let the speed of the boat in still water be x km/hr and the speed of the stream be y km/hr.
Then, speed upstream = (x – y) km/hr
and speed downstream = (x + y) km/hr.
Time taken to cover 16 km upstream


On adding (v) and (vi), we get: 2x = 16 ⇒ x = 8.
On subtracting (vi) from (v), we get:
2y = 8 y = 4.
∴ speed of the boat in still water
= 8 km/hr.
And, speed of the stream = 4 km/hr.
![]()
Question 10.
90% and 97% pure acid solutions are mixed to obtain 21 litres of 95% pure acid Solution: Find the quantity of each type of acid to be mixed to form the mixture.
Solution:
Let the given solutions be labelled as A and B respectively.
Let x litres of A be mixed with y litres of B. Then,
x + y = 21
Quantity of acid in x litres of A = (90% of x)
![]()

⇒ 90x + 97y – 1995 …….(ii)
Multiplying (i) by 90 and subtracting the result from (ii), we get:
7y = 105 ⇒ y = 15.
Putting y = 15 in (i), we get:
x + 15 = 21 = x = 6.
∴ x = 6 and y = 15.
So, 6 litres of 90% solution is mixed with 15 litres of 97% Solution.
![]()
Question 11.
On selling a tea-set at 5% loss and a lemon-set at 15% gain, a shopkeeper gains ₹ 84. However, if he sells the tea-set at 5% gain and the lemon-set at 10% gain, he gains ₹ 104. Find the price of the tea-set and that of the lemon-set paid by the shopkeeper.
Solution:
Let the CP of the tea-set and the lemon-set be ₹ x and ₹ y respectively.

On adding (i) and (ii), we get:
5y = 3760 ⇒ y = 752.
Putting y = 752 in (ii), we get:
x + (2 × 752) = 2080
x = (2080 – 1504) = 576.
∴ x = 576 and y = ₹ 752.
Hence, CP of the tea-set = ₹ 576
and CP of the lemon-set = ₹ 752.
![]()
Question 12.
A chemist has one solution containing 50% acid and a second one containing 25% acid. How much of each should be used to make 10 litres of a 40% acid solution ?
Solution:
Let x liters of 50% solution be mixed with y liters of 25% Solution. Then,
x + y = 10 and 50% of x + 25% of y = 40% of 10
⇒ x + y 10 and \(\frac {50}{100}\) × x + \(\frac {25}{100}\) × y = \(\frac {40}{100}\) × 10
⇒ x + y 10 and \(\frac {x}{2}\) + \(\frac {y}{4}\) = 4
⇒ x + y = 10 …(i)
and 2x + y = 16 …(ii)
On solving (i) and (ii), we get: x = 6 and y = 4.
∴ 6 litres of 50% solution is to be mixed with 4 litres of 25% Solution.
![]()
Question 13.
In a ∆ABC, ∠C = 3∠B = 2(∠A + ∠B). Find the angles.
Solution:
Let ∠A = x° and ∠B = y°. Then,
∠C = 3∠B = (3y)°.
Now, ∠A + ∠B + ∠C = 180°
⇒ x + y + 3y = 180°
x + 4y = 180 ……(i)
Also, ∠C = 2(∠A + ∠B)
⇒ 3y = 2(x + y)
⇒ 2x – y = 0 ……(ii)
Multiplying (ii) by 4 and adding the result to (i), we get:
9x = 180 ⇒ x = 20.
Putting x = 20 in (i), we get:
20 + 4y = 180 ⇒ 4y = 160
⇒ y = \(\frac {160}{4}\) = 40.
∴ x = 20 and y = 40.
∴ ∠A = 20°, ∠B = 40°
and ∠C = (3 x 40)° = 120°.
![]()